什么是IEEE754标准

1985年, IEEE754标准问世，提供了以二进制的方式存储十进制浮点数的具体标准。

IEEE754提供了四种精度规范, 其中最常用的是单精度浮点型 和双精度浮点型 , IEEE754并没有规定float和double表示单精度浮点型和双精度浮点型，但一般提到float、double指的就是单精度、双精度型。

浮点数的存储方式

32位单精度浮点数

32位浮点数（也叫单精度浮点数、float类型）被划分为三部分：

• sign: 1bit符号位，0表示正数，1表示负数

• exponent: 8bit偏移后的指数位，用于表示以2为底的指数，范围为[-127, 128]

  为了表示方便，指数位有一个固定的偏移量(bias)，用于使指数+偏移量=非负数，在32位浮点数中，偏移量为127，在64位浮点数中，偏移量为1023

  例：如果指数为-127，则该8bit为-127+127=0；如果指数为-10，则该8bit为-10+127=117

  个人理解：8bit二进制数表示范围为[0, 255]，既不想要符号位又想表示负数，所以此处有偏移量概念，即将[0, 255]的表示范围转换为[-127, 128]

• fraction: 23bit尾数位

  • 以二进制存储十进制浮点数时，首先要把十进制转换为二进制
  • 以20.5为例，二进制为10100.1，将该数转换为二进制指数形式：1.01001 * 2^4，小数点放在左边第一位和第二位中间，且第一位不能为0，这个过程叫规范化(normalized)，则1.01001为尾数，4为偏移前的指数(unbiased exponent)，偏移后的指数(biased exponent)为4+127=131，131的二进制为10000011
  • 隐藏高位1：由于经过规范化后，小数点前必定为1，所以在存储尾数时，可以省略小数点前的1，节约1bit空间，此处只需记录剩余尾数部分01001
  • 低位补零：在隐藏高位后，尾数为01001，只有5bit，其余低位补零即可，则20.5最终的32位浮点数表示为：0100 0001 1010 0100 0000 0000 0000 0000或0x41A40000

已知浮点数表示，求其十进制数，计算方法如图：

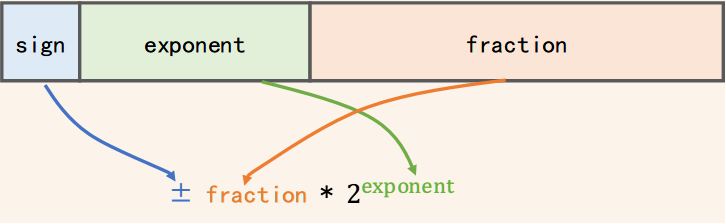
64位双精度浮点数

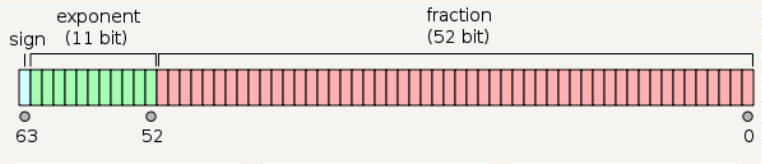
原理同上

浮点数的取指范围

维基百科给出的取值范围

下图是维基百科给出的32位和64位浮点数的十进制取指范围：

32位浮点数的十进制有效数字大约为7位，64位的有效数字大约为16位

前置概念

normal number、subnormal number

IEEE754规定，尾数的隐藏位为1则为normal number（规格数），为0则为subnormal number（非规格数）

一般来说，尾数隐藏位为1的数为规格数，即正常的数

当指数位全0时，表示该数为非规格数，即尾数隐藏位为0

non-number

IEEE754规定指数位全1的数为non-number（特殊数）

指数位全1时，指数为128，即该数为infinity(无穷)，或NaN(Not a Number)

计算方法

根据上述概念，讨论浮点数取值范围时，讨论的是normal number取值范围，即不包括指数位全0和全1的特殊情况

此时的指数位取值范围为[1, 254]，代表的指数范围为[-126, 127]

尾数隐藏位始终为1，所以尾数表示范围为[1.000...000, 1.111...111]，即十进制的[1, 2)

则32位浮点数的取值范围为：

注意开闭区间

将上式的以2为底换成以10为底，省略掉多余的小数，就得到上方维基百科给出的取值范围

补充

下图表示32位单精度浮点数取指范围示意图：

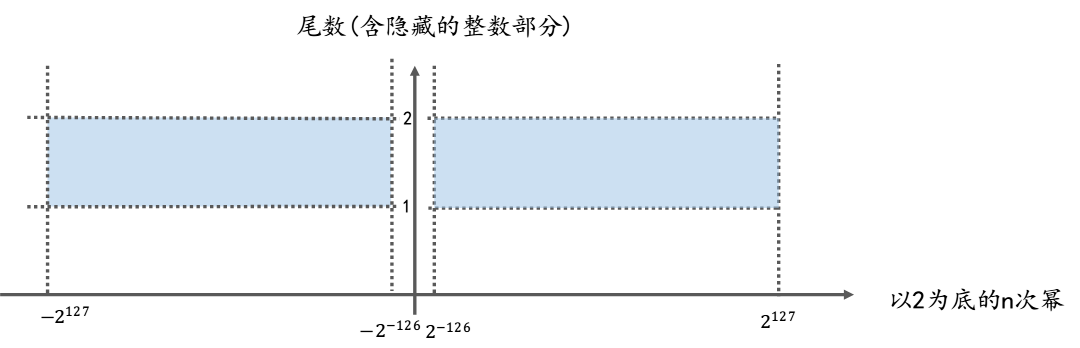
可以看到，normal number的取值范围不包括0以及周围小范围的数

后续

有待补充~